DFS와 BFS

탐색 알고리즘에 대해서 알아볼 것이다. 그래프의 탐색의 목적은 모든 정점을 1번씩 방문 하는 것이다.

DFS (깊이 우선 탐색)

깊이 우선 탐색은 한 방향으로 갈 수 있는 만큼 깊이가기때문에 깊이 우선 탐색이다. 일반적으로 DFS 탐색방법에서는 스택(stack)자료구조를 이용한다.

백트래킹(Backtracking)

탐색 과정에서 무한히 깊이가는 것을 방지하기 위해서 깊이제한(depth bound)을 둔다. depth bound에 도달할 때까지 목표(노드)가 발견되지 않으면 그 전에 탐색한 노드의 부모 노드로 되돌아온다. 이렇게 되돌아 오는 과정을 **백트래킹(Backtracking)**이라 한다.

탐색과정

최대한 깊숙히 많은것을 탐색할 때 사용하며, 스택을 사용한다.

• 스택을 이용해 갈 수 있는 만큼 최대한 많이가고, 갈 수 없으면 이전 정점으로 돌아온다.(백트랙킹)

• 방문한 곳은 표시를 해둔다.(check[i] )

• 이미 방문한 곳은 건너띄고, 갈 수 있는 곳으로 간다. 스택이 비워질 때까지 계속 pop을 한다. 스택이 비어있으면 DFS탐색이 종료된다.

장단점

장점

• 현재 경로상의 노드들만 기억하면 되므로 저장공간의 소요가 비교적 적다.

• 목표노드가 깊은 단계에 있을 경우에 해를 빨리 구할 수 있다.

단점

• 해가 없는 경로에 너무 깊이 빠지게 될 가능성이 잇다. 따라서 실제 경우에는 미리 지정한 임의의 깊이(depth bound)까지만 탐색하고 목표노드를 발견하지 못하면 다음 경로를 따라 탐색하는 것이 유용할 수 있다.

• 얻어진 경로가 최단 경로가 아닐 수 있다. 목표까지의 경로가 여러개인 문제에 대해서 DFS는 목표에 도달하면 탐색을 종료하므로, 이때 찾은 경로는 최적의 경로가 아닐 수 있다.

구현

그래프가 disconnected이거나 혹은 방향 그래프라면 DFS에 의해서 모든 노드가 방문되지 않을 수 있다.

슈도코드

 DFS(G, v)
    visited[v] <- yes
    for each node adjacent to x do                                                                        
        if visited[v] = NO then
            DFS(G, u);
    end
end

인접행렬 구현

dfs(x)는 x를 방문했다는 의미이다. 재귀 호출을 이용해서 구현할 수 있다.

void dfs(int x){
    check[x] = true; //방문한 것 표시
    printf("%d ",x);
    //다음 정점 방문
    for(int i=1;i<=n;i++){
        //간선이 있고, 방문을 하지 않았을 경우
        if(a[x][i]==1 && check[i]==false) dfs(i);
    }
}

//인접행렬 백트릭킹 기법
//반복문 n^2번 실행
bool visited[101];
void dfs(int k)
{
	for(int i=0;i<=n;i++)
	    if(G[k][i] && !visited[G[k][i]])
        {
        	visited[G[k][i]]=true;
            dfs(G[k][i]);
        }
    return;
}

• 시간복잡도 : V*O(V) = O(V^2)

인접리스트 사용

항상 있는 간선만 저장한다.

void dfs(int x){
    check[x] = true; //방문한 것 표시
    printf("%d ",x);
    //다음 정점 방문
    // a[x]는 x와 연결된 정점이다.
    for(int i=1;i<a[x].size();i++){
        int y = a[x][i];
        if(check[y]==false)dfs(y);
    }
}

//인접리스트 백트랙킹 기법
//반복문 m번실행
bool visited[101];
void dfs(int k)
{
	for(int i=0;i<G[i].size();i++)
	    if(!visited[G[k][i].to])
        {
        	visited[G[k][i].to]=true;
            dfs(G[k][i]);
        }
    return;
}

• 모든 정점을 한번씩 거치고 모든 간선을 한번씩 검사하게 된다.

• 시간복잡도 O(V+E)

BFS (너비 우선 탐색)

현재 정점에서 깊이가 1인 정점을 모두 탐색한 뒤 깊이를 늘려가는 방식이다. 너비우선탐색은 백트랙을 하지 않는다. 대신에 현재 정점에서 깊이가 1인 정점을 모두 방문해야하므로 **큐(queue)**라는 FIFO(First In First Out)자료구조를 활용해 현재 정점에서 깊이가 1 더 깊은 모든 정점을 순차적으로 큐에 저장해 탐색에 활용한다.

std::queue()를 활용하는 방법을 익힐 필요가 있다.

BFS를 하면서 각 노드에 대해서 최단 경로의 길이를 구할 수 있다.

탐색과정

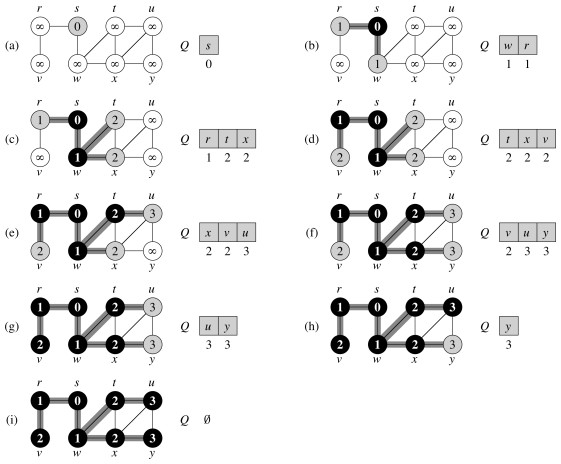
• L0 = {s}, s는 출발 노드

• L1 = L0의 모든 이웃 노드들

• L2 = L1에서 모든 이웃들 중 L0에 속하지 않는 노드들

• ...

• LN = Ln에서 모든 이웃들 중 Ln-1에 속하지 않는 노드들

다음과 같은 순서로 방문하는 방법이다.

Queue

최대한 넓게 가는길을 탐색할 때 사용하며, 큐를 사용한다. 큐를 이용해서 지금 위치에서 갈 수 있는 것을 모두 큐에 넣는 방식이다.

• BFS는 큐에 넣을 때 방문했다고 체크(check[i])해야한다.

  • 큐에서 pop한 노드들 중에서 방문하지 않은 모든 이웃 노드를 큐에 넣으면서 방문했다고 체크해준다.

  • Queue가 빌때까지 진행해준다.

구현

그래프가 disconnected이거나 혹은 방향 그래프라면 BFS에 의해서 모든 노드가 방문되지 않을 수 있다.

슈도코드

BFS(G, s)// 그래프 G와 출발 노드 s
    Q <- ø; // 큐를 하나 생성
    Enqueue(Q,s);
    while Q!=ø do
        u <- Dequeue(Q)
        for each v adjacent to u do                                                                     
            if v is unvisited then
                mark v is visited;
                Enqueue(Q,v);
            end;
        end;
    end;
 

인접 행렬

queue<int> q;
check[1]= true;
q.push(1);
while(!q.empty()){
    int x = q.front;
    q.pop();
    printf("%d ",x);
    //다음 정점을 찾기
    for(int i=1;i<=n;i++){
        if(a[x][i]==1&&check[i]==false){
            check[i]=true;
            q.push(i);
        }
    }
}

//인접행렬
bool visited[101];

void bfs(int k)
{
	std::queue<int> Q;
    Q.push(k), visited[k]=1;
    while(!Q.empty())
    {
    	int current = Q.front();Q.pop();
        for(int i=0;i<G[current].size();i++)
        	if(G[current][i]&&!vistited[G[current][i]])
            {
            	visited[G[current][i]]=1;
                Q.push(G[current][i]);
            }
    }
}

전체 탐색하는데 있어서 반복문을 n^2번 실행하게된다.

• 시간복잡도 O(V^2)

인접 리스트

queue<int> q;
check[1]= true;
q.push(1);
while(!q.empty()){
    int x = q.front;
    q.pop();
    printf("%d ",x);
    //다음 정점을 찾기
    for(int i=1;i<a[x].size;i++){
        int y = a[x][i];
        if(check[y]==false){
            check[y]=true;
            q.push(i);
        }
    }
}

//인접리스트에 저장했을 경우
#include <queue>
bool visited[101];

void bfs(int k)
{
	std::queue<int> Q;
    Q.push(k), visited[k]=1;
    while(!Q.empty())
    {
    	int current = Q.front();Q.pop();
        for(int i=0;i<G[current].size();i++)
        	if(!vistited[G[current][i]])
            {
            	visited[G[current][i]]=1;
                Q.push(G[current][i]);
            }
    }
}

전체를 탐색하는 데 있어서 반복문을 m번 실행하게 된다.

최단 경로

• 입력 : 방향 혹은 무방향 그래프 G(V,E), 그리고 출발노드 s

• 출력 : 모든 노드 v에 대해서

  • d[v] = s로부터 v까지의 최단 경로의 길이(엣지의 수)

  • π[v] = s로부터 v까지의 최단 경로상에서 v의 직전 노드(predecessor)

BFS(G, s)// 그래프 G와 출발 노드 s
    Q <- ø;
    d[v]<-0;
    π[v]<-null;
    Enqueue(Q,s);
    while Q!=ø do
        u <- Dequeue(Q)
        for each v adjacent to u do                                                                      
            if v is unvisited then //일반적으로 방문하지 않은 것은 -1로 넣어두고 구한다.
                mark v is visited;
                d[v]<-d[u]+1;
                π[v]<-u;
                Enqueue(Q,v);
            end;
        end;
    end;
 

// 최단경로 출력
PRINT-PATH(G,s,v)
    if v=s then
        print s;
    else if π[v] = null then
        print "no path from s to v exists";                                                               
    else
        PRINT-PATH(G,s,π[v]);
        print v;
    end.

시간복잡도

• 시간복잡도 O(V+E)

DFS vs BFS

	DFS	BFS
동작 원리	스택	큐
구현 방법	재귀	큐 자료구조 이용

문제풀어보기

DFS와 BFS

그래프를 DFS로 탐색한 결과와 BFS로 탐색한 결과를 출력하는 프로그램을 작성하시오. 단, 방문할 수 있는 정점이 여러 개인 경우에는 정점 번호가 작은 것을 먼저 방문하고, 더 이상 방문할 수 있는 점이 없는 경우 종료한다. 정점 번호는 1번부터 N번까지이다.

#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
#include <queue>

using namespace std;
vector<int> a[1001];
bool check[1001];


void dfs(int node) {
    check[node] = true;
    printf("%d ",node);
    for (int i=0; i<a[node].size(); i++) {
        int next = a[node][i];
        if (check[next] == false) {
            dfs(next);
        }
    }
}

void bfs(int start) {
    queue<int> q;
    //memset은 메모리를 초기화 하는 함수
    //1번 파라미터는 값을 복사할 곳이고, 2번 파라미터는 초기화할 값, 마지막은 얼마만큼의 메모리를 초기화 할 것인지 하는 크기이다.
    memset(check,false,sizeof(check));
    check[start] = true;
    q.push(start);
    while (!q.empty()) {
        int node = q.front();
        q.pop();
        printf("%d ",node);
        for (int i=0; i<a[node].size(); i++) {
            int next = a[node][i];
            if (check[next] == false) {
                check[next] = true;
                q.push(next);
            }
        }
    }
}
int main() {
    int n, m, start;
    scanf("%d %d %d",&n,&m,&start);
    for (int i=0; i<m; i++) {
        int u,v;
        scanf("%d %d",&u,&v);
        a[u].push_back(v);
        a[v].push_back(u);
    }
    for (int i=1; i<=n; i++) {
        sort(a[i].begin(), a[i].end());
    }
    dfs(start);
    puts("");
    bfs(start);
    puts("");
    return 0;
}

DFS

flood_fill

지뢰찾기, 뿌요뿌요 등 게임에서 많이 활용되는 알고리즘. 재귀함수를 이용해 깊이우선탐색을 구현한다. 하지만 재귀의 깊이가 너무 커지면 runtime error가 발생할 수 있다. 깊이가 너무 크다고 판단되면 너비우선탐색으로 처리하거나 재귀대신 스택을 이용한다.

dfs함수 부분의 4방향 탐색을 dx,dy를 이용해 작성할 수 있다.

int dx[4]={1,0,-1,0},dy[4]={0,1,0,-1};

void dfs(int a, int b, int c)
{
	A[a][b]=c;
    for(int i=0;i<4;i++)
    	if(safe(a+dx[i],b+dy[i])&&A[a+dx[i]][b+dy[i]]==1)
        	dfs(a+dx[i],b+dy[i],c);
}

n-queen

n*n체스 보드판에 n개의 queen을 서로 공격하지 못하도록 배치하는 방법을 찾아내는 문제. 대각선 검사하면서 가야하는 알고리즘에 유용하다.

• 퀸은 8방향으로 모두 공격할 수 있다.

  1. 첫 번째 행, 첫 번째 열에 퀸을 놓는다.

  2. 다음 행에서 가능한 가장 왼쪽 열에 퀸을 놓는다.

  3. n번째 열에 더 이상 퀸을 놓을 수 없다면 백트랙한다.

  4. 마지막 행에 퀸을 놓으면 하나의 해를 구한 것이다.

  5. 모든 경우를 조사할 때까지 백트래킹해가며 해들을 구한다.

깊이우선탐색을 하며 해를 구할 때마다 카운트해 원하는 해를 구할 수 있다. 열과 대각선만 검사하면 된다. 대각선은 행+열 위치에 체크해 기울기가 증가하는 대각선 상에 퀸을 놓을 수 있는지 없는지 확인한다. 기울기가 감소하는 대각선은 행과 열의 차가 일정하다. n+(행-열)의 위치에 체크. 백트랙 시에 가장 중요한 점은 체크배열에 기록해 두었던 체크를 모두 해제해야한다.