Heap

힙(heap)은 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 **완전이진트리(Complete binary tree)**를 기본으로 한 자료구조(tree-based structure)이다. (위키백과 )

응용

1. Heap Sort 정렬 알고리즘
2. Priority Queue
3. Graph Algorithm : Dijkstra, Prim's Minimum Spanning Tree(프림 최소 신장 트리)

그리고 다양한 문제를 푸는데에서 사용된다.

규칙

최소 힙(min heap)

부모노드의 키값이 자식노드의 키값보다 항상 작거나 같다. key(부모노드) < key(자식노드)

최대 힙(max heap)

부모노드의 키값이 자식노드의 키값보다 항상 크거나 같다. key(부모노드) > key(자식노드)

따라서 루트노드에는 항상 가장 큰 값이나 가장 작은 값이 저장되어 있기때문에 최대값 또는 최솟값을 O(1)만에 찾을 수 있다. 여기서 키값은 오로지 부모 자식노드간에만 성립한다.

Height/Depth

n개의 노드를 가지고 있는 heap의 높이는 O(logn)이다. 힙은 완전이진트리이므로 노드의 개수로 깊이와 높이를 계산할 수 있다.

마지막 level을 제외하고는 각 레벨 i에 2^i개의 노드가 존재한다.

구현

배열

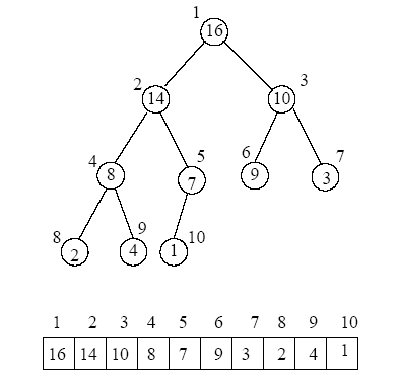
힙은 완전이진트리이므로 각 노드에 번호를 붙일 수 있다. 배열은 완전이진트리를 표현하기에 매우 효율적이다.

배열로 표현함으로써 부모노드와 자식노드를 찾기가 쉬워진다.

• 왼쪽 자식노드 인덱스 : 2*(부모노드 인덱스)

• 오른쪽 자식노드 2*(부모노드 인덱스)+1

• 노드 x의 부모 노드 인덱스는 (자식노드 인덱스)/2로 알 수 있다.

주의사항 **index는 1부터 시작!**한다는 점을 주의해야한다.

삽입(upheap)

1. 가장 끝의 자리에 노드를 삽입한다.

2. 그 노드와 부모 노드를 서로 비교한다.

3. 규칙(최소힙, 최대힙)에 맞으면 그대로 두고, 그렇지 않으면 부모와 교환한다.

4. 규칙에 맞을 때까지 1~3번 과정을 반복한다.

시간복잡도

• O(logn)

삭제(downheap)

최댓값 혹은 최솟값이 저장된 루트 노드만 제거할 수 있다.

1. 루트 노드를 제거한다.

2. 루트 자리에 가장 마지막 노드를 삽입한다.

3. 올라간 노드와 그의 자식 노드(들)와 비교한다.

4. 조건에 만족하면 그대로 두고, 그렇지 않으면 자식과 교환한다.

• 최대 힙

  1. 부모보다 더 큰 자식이 없으면 교환하지 않고 끝낸다.

  2. 부모보다 더 큰 자식이 하나만 있으면 그 자식하고 교환하면 된다.

  3. 부모보다 더 큰 자식이 둘 있으면 자식들 중 큰 값과 교환한다.

• 최소 힙

  1. 부모보다 더 작은 자식이 없으면 교환하지 않고 끝낸다.

  2. 부모보다 더 작은 자식이 하나만 있으면 그 자식하고 교환하면 된다.

  3. 부모보다 더 작은 자식이 둘 있으면 자식들 중 작은 값과 교환한다.

1. 조건을 만족할 때까지 4의 과정을 반복한다.

시간복잡도

• O(logn)

구현

최소힙

#include <stdio.h>
#define MAX 1000000

typedef struct{
    int heap[MAX];
    int hsize;
}Heap;

void init(Heap * h){
    h->hsize=0;
}

void insert(Heap * h, int key){
    int p; //현재 위치 저장
    
    // 마지막 위치에 추가
    h->heap[++(h->hsize)]=key;
    
    // 위치 조정
    p=h->hsize;
    while((h->heap[p/2])>key){
        h->heap[p] = h->heap[p/2];
        p/=2;
    }
    h->heap[p]=key;
}

int delete(Heap * h){
    int min,last,child,i;
    
    //루트노드값이 최소
    min = h->heap[1];
    last = h->heap[(h->hsize)--];
    
    for(i=1; i*2<=h->hsize; i=child){
        child = i*2;
        if(child!=h->hsize && h->heap[child+1]<h->heap[child])child++;
        if(last>h->heap[child])h->heap[i]=h->heap[child];
        else break;
    }
    h->heap[i]=last;
    return min;
}


int main(int argc, const char * argv[]) {
    
    Heap heap;
    int min;
    init(&heap);
    insert(&heap, 10);
    insert(&heap, 5);
    insert(&heap, 30);
    
    for(int i=1;i<=heap.hsize;i++){
        printf("%d ",heap.heap[i]);
    }
    min = delete(&heap);
    printf("\n%d \n",min);
    for(int i=1;i<=heap.hsize;i++){
        printf("%d ",heap.heap[i]);
    }
    min = delete(&heap);
    printf("\n%d \n",min);
    for(int i=1;i<=heap.hsize;i++){
        printf("%d ",heap.heap[i]);
    }
    
    
    return 0;
}

최대힙

#include <stdio.h>
#define MAX 100

typedef struct{
    int heap[MAX];
    int hsize;
}Heap;

void init(Heap * h){
    h->hsize=0;
}

void insert_max(Heap * h, int key){
    int p; //현재 위치 저장
    
    p=++(h->hsize);
    // 마지막 위치에 추가
    h->heap[p]=key;
    
    
    // 위치 조정
    while((h->heap[p/2])<key){
        if(p==1)break;
        h->heap[p] = h->heap[p/2];
        p/=2;
    }
    h->heap[p]=key;
}
int delete_max(Heap * h){
    int max,last,child,i;
    
    //루트노드값이 최소
    max = h->heap[1];
    last = h->heap[(h->hsize)--];
    
    for(i=1; i*2<=h->hsize; i=child){
        child = i*2;
        if(child!=h->hsize && h->heap[child+1]>h->heap[child])child++;
        if(last<h->heap[child])h->heap[i]=h->heap[child];
        else break;
    }
    h->heap[i]=last;
    return max;
}


int main(int argc, const char * argv[]) {
    
    Heap heap;
    int max;
    init(&heap);
    insert_max(&heap, 10);
    insert_max(&heap, 5);
    insert_max(&heap, 30);
    
    for(int i=1;i<=heap.hsize;i++){
        printf("%d ",heap.heap[i]);
    }
    max = delete_max(&heap);
    printf("\n%d \n",max);
    for(int i=1;i<=heap.hsize;i++){
        printf("%d ",heap.heap[i]);
    }
    max = delete_max(&heap);
    printf("\n%d \n",max);
    for(int i=1;i<=heap.hsize;i++){
        printf("%d ",heap.heap[i]);
    }
    
    
    return 0;
}