1.0.0

Huffman Coding

허프만 부호화(Huffman coding)는 무손실 압축에 쓰이는 엔트로피 부호화의 일종으로, 데이터 문자의 등장 빈도에 따라서 다른 길이의 부호를 사용하는 알고리즘이다.

  • 압축이란 엄청나게 큰 문제(많은 비트를 필요로 하는)의 정보를 고스란히 표현하면서도 전체 비트량을 줄일 수 있는 효과적인 부호화 기술의 과정이다.

  • 무손실 압축은 데이터 압축의 일종으로 손실 압축의 반대말이다. 원래의 정보를 그대로 보존해야 하기 때문에, 정보 엔트로피의 한계가 그대로 반영된다. 여기에서 정보 엔트로피의 한계란 개별 정보의 확률값에 의하여 계산되는 값이 아닌, 전체 신호의 상관관계를 반영한 한계값이다.

  • 엔트로피 인코딩 or 엔트로피 부호화(entropy encoding) : 심볼이 나올 확률에 따라 심볼을 나타내는 코드의 길이를 달리하는 부호화 방법

    • 엔트로피는 각 기호가 포함하는 평균 정보량을 의미

    • Shannon 부호화 이론에서는 엔트로피를 우리가 할 수 있는 최선이라 말한다.

    • 자주 발생하는 기호를 찾아내는 데 목적이있다.

  • 가변 길이 부호화(VLC) : 더 자주 발생하는 기호는 더 적은 비트로 부호화

    • 즉, 자주 발생하는 기호는 빨리 전송될 수 있는 코드(적은 비트), 자주 발생하지 않는 것은 긴 코드가 부여된다.

허프만 알고리즘의 부호화 순서는 아래에서 위로 진행하는 방법이다.

알고리즘

  1. 초기화 : 모든 기호를 출현 빈도수에 따라 나열한다.

  2. 단 한 가지 기호가 남을 때까지 아래 단계를 반복한다.

    1. 목록으로부터 가장 빈도가 낮은 것을 2개 고른다.

    2. 허프만이 두 가지 기호를 부모 노드를 가지는 부트리를 구성하고 자식 노드르 생성한다.

    3. 부모 노드 단 기호들의 빈도수를 더하여 주 노드에 할당하고 목록의 순서에 맞도록 목록에 삽입한다.

    4. 목록에서 부모노드에 포함된 기호를 제거한다.

  3. 루트노드로부터의 경로에서 각 가지에 코드워드를 부여한다.

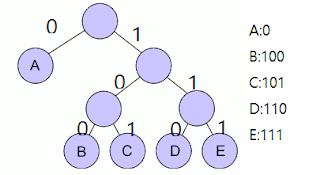
허프만 알고리즘은 입력 기호를 리프 노드로 하는 이진 트리를 만들어서 접두 부호를 만들어 내는 알고리즘이다.

구현

Huffman 알고리즘은 최소빈도 수를 출력하기 위해서 우선 순위 큐를 필요로한다. 최소힙을 사용해서 구현해보았다.

구조체

// 기본적으로 노드는 data정보와 빈도수는 음수가아닌 int값을 갖는다.
// 허프만은 이진트리 구조이므로 left와 right의 포인터를 갖고있다.
typedef struct node{
    char data;
    unsigned int frequency;
    struct node * left, *right;
}Node;

// heap는 heap의 크기, node array를 갖고있다.
// capacity는 배열의 크기를 말한다.
typedef struct heap{
    unsigned int size;
    unsigned int capacity;
    Node ** array;
}Heap;

new_node

Node * new_node(char data, unsigned freq){
    Node * new = (Node*)malloc(sizeof(Node));
    
    new->data=data;
    new->frequency=freq;
    new->left=new->right=NULL;
    
    return new;
}

Heap 초기화

Heap * init(unsigned capacity){
    Heap * heap = (Heap*)malloc(sizeof(Heap));
    
    // 현재 heap의 크기는 0이다.
    heap->size=0;
    heap->capacity=capacity;
    // 배열의 크기 만큼 공간을 할당해준다.
    heap->array = (Node**)malloc(heap->capacity*sizeof(Node*));
    
    return heap;
}

heapify

두 개의 subtree가 min heap일때 root에 추가된 노드를 포함한 전체가 heap의 조건을 만족하도록 각 노드의 위치를 조정

void swap_node(Node ** a, Node ** b){
    Node * tmp = *a;
    *a = *b;
    *b = tmp;
}

// heapify : 두 개의 subtree가 min heap일때 root에 추가된 노드를 포함한 전체가
// heap을 만족하도록 각 노드의 위치를 조정
void heapify(Heap * h, int i){
    int min = i;
    int left = 2*i +1;    // 왼쪽 자식노드
    int right = 2*i+2;    // 오른쪽 자식노드
    
    // 왼쪽 자식 노드의 인덱스가 heap의 크기보다 작고
    // frequency값이 최소값의 frequency보다 작으면 최소값을 left로 변경
    if(left < h->size && h->array[left]->frequency < h->array[min]->frequency)min=left;
    // 오른쪽 자식노드도 마찬가지
    if(right < h->size && h->array[right]->frequency < h->array[min]->frequency)min=right;
    // 만약 최소값이 i와 다르다면 노드위치를 변경해준다.
    if(min!=i){
        swap_node(&h->array[min], &h->array[i]);
        heapify(h,min);
    }
}

delete

Node * delete(Heap * h){
    Node * tmp = h->array[0];
    h->array[0]=h->array[--h->size];
    heapify(h, 0);
    return tmp;
}

insert

void insert(Heap * h, Node * node){
    int p; //현재 위치 저장
    
    // 마지막 위치에 추가
    p=++h->size-1;;
    
    // 위치 조정
    while(node->frequency < h->array[(p-1)/2]->frequency){
        h->array[p] = h->array[(p-1)/2];
        p=(p-1)/2;
    }
    h->array[p]=node;
}

heap 생성

void build_heap(Heap * h){
    int n = h->size-1;
    int i;
    for(i=(n-1)/2;i>=0;i--)
        heapify(h, i);
}

Heap * create_heap(char data[], int freq[],int size){
	//초기화해서 생성한다.
    Heap * heap = init(size);
    
    // 빈도수와 데이터값을 넣은 노드를 생성해준다.
    for(int i=0;i<size;i++)
        heap->array[i]=new_node(data[i], freq[i]);
    
    heap->size = size;
    build_heap(heap);
    return heap;
}

출력

//배열 원소 값 출력
void print(int arr[],int n){
    for(int i=0;i<n;i++)
        printf("%d",arr[i]);
    printf("\n");
}
int is_leaf(Node * root){
    return !(root->left) && !(root->right);   
}
// 최종 코드 출력
void print_code(Node * root, int arr[], int top){
	// 왼쪽 자식노드(가지)는 0저장
    if(root->left){
        arr[top]=0;
        print_code(root->left, arr,top+1);
    }
	// 오른쪽 자식노드(가지)는 1저장
    if(root->right){
        arr[top]=1;
        print_code(root->right, arr,top+1);
    }
    // 단말노드면 코드 출력
    if(is_leaf(root)){
        printf("%c: ",root->data);
        print(arr, top);
    }
}

Huffman 생성

// heap의 크기가 1인지 아닌지 검사
int is_one(Heap * h){
    return (h->size==1);
}
Node * build_huffman(char data[],int freq[], int size){
    Node * left, *right, *top;
    
    Heap * heap = create_heap(data, freq, size);
    
    while(!is_one(heap)){
        left = delete(heap);
        right = delete(heap);
        
        top = new_node('$',left->frequency+right->frequency);
        top->left=left;
        top->right= right;
        
        insert(heap, top);
    }
    return delete(heap);
}


void huffman(char data[],int freq[],int size){
    Node * root = build_huffman(data, freq, size);
    
    int arr[MAX],top=0;
    
    print_code(root, arr,top);
}

Main

int main(){
    char arr[] = { 'a', 'b', 'c', 'd', 'e', 'f' };
    int freq[] = { 5, 9, 12, 13, 16, 45 };
    
    int size = sizeof(arr) / sizeof(arr[0]);
    
    huffman(arr, freq, size);   
}

결과

f: 0
c: 100
d: 101
a: 1100
b: 1101
e: 111

응용

  • 팩스

  • JPEG

  • MPEG

PreviousHeapNextPriority Queue

Last updated